DNN的数学原理
前言
数学是现实世界的精确抽象,再花里胡哨的东西,内在终究还是一堆加减乘除。因此,从数学的角度写一下到底啥是深度学习,学过线代就能懂。
神经网络模型的结构
神经网络的基础单元是神经元,多个神经元纵向堆叠形成神经网络层,神经网络层横向堆叠形成神经网络。
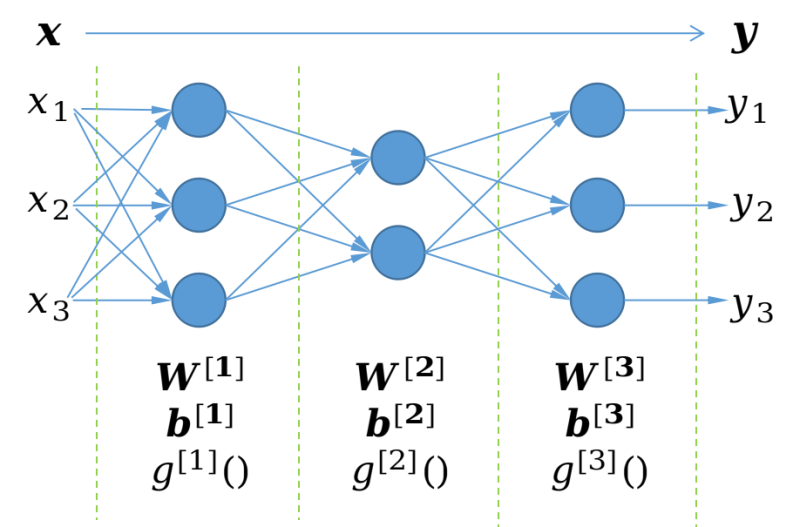
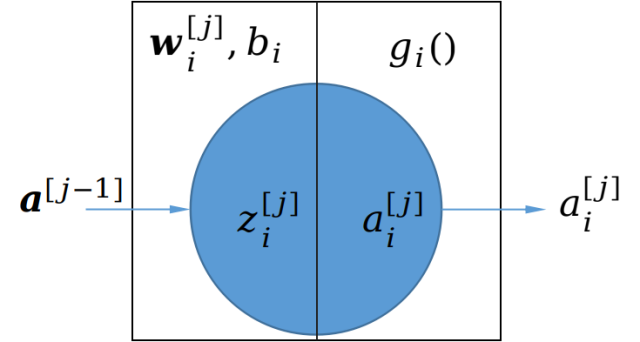
神经元的数学原理
对于一个神经元,进行的数学计算为:
接受一个向量$\boldsymbol{a}^{[j-1]}$,通过与$\boldsymbol{w}^{[j]}_i$进行向量内积运算产生一个中间值$z_i^{[j]}$(标量),然后用激活函数$g_i^{[j]}()$将$z$转换为$a_i^{[j]}$。
其中:
上标用来定位该神经元位于哪一层,一般输入层后的第一层为1;
下标用来定位该神经元位于第几个,一般最上方的序号为0;
矩阵维度确认的数学原理
首先区分开这4个概念:模型的参数,层的参数,神经元的参数,数据及数据的中间值。然后,仔细理解上面两段话,神经网络中最为tricky的维度问题便迎刃而解:
- 对于$\boldsymbol{x}$和$\boldsymbol{y}$,其维度看样本就知道,已经定义好了;
- 对于某一个神经元的权重参数$\boldsymbol{w}^{[j]}_i$,由于要跟输入的向量$\boldsymbol{a}^{[j-1]}$进行内积,所以两者的维度必然是相同的,而后者作为一个列向量,其行数等于上一层的神经元数量(因为每个神经元输出一个标量)。然后由于本层的每一个神经元都有一个权重参数$\boldsymbol{w}^{[j]}$,那么由${\boldsymbol{w}^{[j]}}^T$纵向堆叠形成的${\boldsymbol{W}^{[j]}}^T$的行数就是$\boldsymbol{w}^{[j]}$的个数,亦即本层的神经元数量,其列数前面已经说了,就是$\boldsymbol{w}^{[j]}$的行数,亦即上一层的神经元数量。
- 对于某一个神经元的偏移量参数${b}^{[j]}$,自然是一个标量。那么本层的偏移量参数$\boldsymbol{b}^{[j]}$的行数就是${b}^{[j]}$的数量,亦即本层的神经元数量。
- 对于每一层的中间值$\boldsymbol{z}^{[j]}$,输出值$\boldsymbol{a}^{[j]}$,其维度确定方式与$\boldsymbol{b}^{[j]}$一样。
- 另外对于激活函数,一般同一层都一样,所以$\boldsymbol{g}^{[j]}()$退化为${g}^{[j]}()$。
矢量化的数学原理
矢量化的本质是将样本在时间轴上被神经网络模型处理的序列转化为空间上的序列:
$X= (\boldsymbol{x}^1,\boldsymbol{x}^2, …, \boldsymbol{x}^)$
说人话就是,原来每次送入模型一个列向量,计算得到一个列向量。现在每次送入m个列向量,计算的到m个列向量。当然了,各层的中间值$\boldsymbol{z}^{[j]}$和输出值$\boldsymbol{a}^{[j]}$也都将因此横向扩充一个维度。
Batch的数学原理
一个batch指每次送入模型的一批样本。比如,现有2000个样本,将其划分为4个batch,那么每个batch包含500个样本,即
batch_size=500;
batch_num = 4;
一个epoch指整个训练集被利用了一次。即,2000个样本中的每一个都被代入模型进行了一次前向计算和反向传播。
一个iteration指权重参数更新一次。一个epoch中可能有多个iteration,也可能只有一个iteration,这取决于batch_num的值。
留一个疑问,在一个epoch中,一个batch会循环多次使用吗?还是只用1次就结束了?例如,在一个epoch中用batch_1迭代10次,然后batch_2迭代10次,….,最后batch_4迭代10次,一个epoch完成。是这样吗?——目前来看不是这样,而是只用1次。 2021年7月15日
正向计算的数学原理
正向计算,用于得到所需的预测结果:
- 输入一个列向量:
$\boldsymbol{x} = (x_1, x_2, … , x_n )^T$
进行一系列矩阵计算:
$\boldsymbol{a}^{[0]} = \boldsymbol{x}$
$\boldsymbol{z}^{[1]} = {\boldsymbol{W}^{[1]}}^T\boldsymbol{a}^{[0]}+\boldsymbol{b}^{[1]}$
$\boldsymbol{a}^{[2]} = g^{[1]}(\boldsymbol{z}^{[1]})$
…
$\boldsymbol{z}^{[j]} = {\boldsymbol{W}^{[j]}}^T\boldsymbol{a}^{[j-1]}+\boldsymbol{b}^{[j]}$
$\boldsymbol{a}^{[j]} = g^{[j]}(\boldsymbol{z}^{[j]})$
…
$\boldsymbol{z}^{[l]} = {\boldsymbol{W}^{[l]}}^T\boldsymbol{a}^{[l-1]}+\boldsymbol{b}^{[l]}$
$\boldsymbol{a}^{[l]} = g^{[l]}(\boldsymbol{z}^{[l]})$
$\boldsymbol{\hat{y}} = \boldsymbol{a}^{[l]}$特别地,对于多分类模型的输出层(最后一层),一般有:
$g^{[l]}(\boldsymbol{x}) = softmax(\boldsymbol{x}) = \frac{exp(\boldsymbol{x})}{\boldsymbol{1}^Texp(\boldsymbol{x})}$
其中 $\boldsymbol{1}$ 为全1列向量,维度可从context推得。
- 得到一个列向量:
$\boldsymbol{\hat{y}} = (\hat{y}_1,\hat{y}_2, … , \hat{y}_n)^T$
反向传播的数学原理
反向传播,用于得到各网络层参数的更新量。主要有以下3个步骤:
- 单个样本$\boldsymbol{x}$ 正向计算,得到各层的$\boldsymbol{z}$和$\boldsymbol{a}$备用。
- 计算输出层的参数更新量:
- 求得损失$L$对$\boldsymbol{z}^{[l]}$的偏导$\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}$,记作$d\boldsymbol{z}^{[l]}$。上标$l$表示最后一层,即输出层。若输出层激活函数为$softmax$且损失函数为交叉熵,则有$d\boldsymbol{z}^{[l]} = softmax(\boldsymbol{z}^{[l]}) - \boldsymbol{y}$,对应的求导过程如下:
$L = -\boldsymbol{y}^Tlog\hat{\boldsymbol{y}}$
$\downarrow$
$dL = -d\boldsymbol{y}^Tlog\hat{\boldsymbol{y}}-\boldsymbol{y}^Td(log\hat{\boldsymbol{y}})$
$= -\boldsymbol{y}^T d(log\hat{\boldsymbol{y}})$
$= -\boldsymbol{y}^Td(log(softmax(\boldsymbol{z}^{[l]})))$
$= -\boldsymbol{y}^Td(log(\frac{exp(\boldsymbol{\boldsymbol{z}^{[l]}})}{\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}})}))$
$= -\boldsymbol{y}^Td(log(exp(\boldsymbol{\boldsymbol{z}^{[l]}}))+\boldsymbol{1}log(\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}})))$
$= -\boldsymbol{y}^Td\boldsymbol{z}^{[l]} + d(log(\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}})))$
$= -\boldsymbol{y}^Td\boldsymbol{z}^{[l]} + \frac{d(\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}}))}{\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}})}$
$= -\boldsymbol{y}^Td\boldsymbol{z}^{[l]} + \frac{\boldsymbol{1}^T(exp(\boldsymbol{\boldsymbol{z}^{[l]}}) \odot d\boldsymbol{z}^{[l]} )}{\boldsymbol{1}^Texp(\boldsymbol{\boldsymbol{z}^{[l]}})}$
$= -\boldsymbol{y}^Td\boldsymbol{z}^{[l]} + {\frac{exp(\boldsymbol{\boldsymbol{z}^{[l]}})}{\boldsymbol{1}^Texp(\boldsymbol{z}^{[l]})}}^Td\boldsymbol{z}^{[l]}$
$= (softmax(\boldsymbol{z}^{[l]})-\boldsymbol{y}^T)^Td\boldsymbol{z}^{[l]}$
$\downarrow$
$tr(dL) = dL = tr((softmax(\boldsymbol{z}^{[l]})-\boldsymbol{y}^T)^Td\boldsymbol{z}^{[l]}) = tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td\boldsymbol{z}^{[l]})$
$\downarrow$
$\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}} = softmax(\boldsymbol{z}^{[l]})-\boldsymbol{y}^T$
$\downarrow$
$d\boldsymbol{z}^{[l]} = softmax(\boldsymbol{z}^{[l]})-\boldsymbol{y}^T$ - 利用微分的分解+迹技巧实现链式法则,由$d\boldsymbol{z}^{[l]}$得到$d{\boldsymbol{W}^{[l]}}^T$,$d\boldsymbol{b}^{[l]}$,$d\boldsymbol{a}^{[l-1]}$
- $d{\boldsymbol{W}^{[l]}}^T$的求导过程如下:
$tr(dL) = tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td\boldsymbol{z}^{[l]})$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td({\boldsymbol{W}^{[l]}}^T\boldsymbol{a}^{[l-1]}+\boldsymbol{b}^{[l]}))$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td{\boldsymbol{W}^{[l]}}^T\boldsymbol{a}^{[l-1]})$
$= tr(\boldsymbol{a}^{[l-1]}{\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td{\boldsymbol{W}^{[l]}}^T)$
$= tr(({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}{\boldsymbol{a}^{[l-1]}}^T)^Td{\boldsymbol{W}^{[l]}}^T)$
$\downarrow$
$\frac{\partial{L}}{\partial{\boldsymbol{W}^{[l]}}^T} = {\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}{\boldsymbol{a}^{[l-1]}}^T$
$\downarrow$
$d{\boldsymbol{W}^{[l]}}^T = d\boldsymbol{z}^{[l]}{\boldsymbol{a}^{[l-1]}}^T$ - $d\boldsymbol{b}^{[l]}$的求导过程
$tr(dL) = tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td\boldsymbol{z}^{[l]})$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td({\boldsymbol{W}^{[l]}}^T\boldsymbol{a}^{[l-1]}+\boldsymbol{b}^{[l]}))$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td\boldsymbol{b}^{[l]})$
$\downarrow$
$\frac{\partial{L}}{\partial{\boldsymbol{b}^{[l]}}} = {\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}$
$\downarrow$
$d\boldsymbol{b}^{[l]} = d\boldsymbol{z}^{[l]}$ - $d\boldsymbol{a}^{[l-1]}$的求导过程如下:
$tr(dL) = tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td\boldsymbol{z}^{[l]})$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^Td({\boldsymbol{W}^{[l]}}^T\boldsymbol{a}^{[l-1]}+\boldsymbol{b}^{[l]}))$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}^T{\boldsymbol{W}^{[l]}}^Td\boldsymbol{a}^{[l-1]})$
$= tr((\boldsymbol{W}^{[l]}\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}})^Td\boldsymbol{a}^{[l-1]})$
$\downarrow$
$\frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}} = {\boldsymbol{W}^{[l]}\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}}$
$\downarrow$
$d\boldsymbol{a}^{[l-1]} = \boldsymbol{W}^{[l]}d\boldsymbol{z}^{[l]}$
- $d{\boldsymbol{W}^{[l]}}^T$的求导过程如下:
- 利用微分的分解+迹技巧实现链式法则,由$d\boldsymbol{a}^{[l-1]}$得到$d\boldsymbol{z}^{[l-1]}$,对应的求导过程如下:
$tr(dL) = tr({\frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}}}^Td\boldsymbol{a}^{[l-1]})$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}}}^Td(g(\boldsymbol{z}^{[l-1]}))$
$= tr({\frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}}}^T(g’(\boldsymbol{z}^{[l-1]}) \odot d\boldsymbol{z}^{[l-1]}))$
$= tr((\frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}} \odot g’(\boldsymbol{z}^{[l-1]}))^T d\boldsymbol{z}^{[l-1]})$
$\downarrow$
$\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l-1]}}} = \frac{\partial{L}}{\partial{\boldsymbol{a}^{[l-1]}}} \odot g’(\boldsymbol{z}^{[l-1]})$
$\downarrow$
$d\boldsymbol{z}^{[l-1]} = d\boldsymbol{a}^{[l-1]}\odot g’(\boldsymbol{z}^{[l-1]})$
- 求得损失$L$对$\boldsymbol{z}^{[l]}$的偏导$\frac{\partial{L}}{\partial{\boldsymbol{z}^{[l]}}}$,记作$d\boldsymbol{z}^{[l]}$。上标$l$表示最后一层,即输出层。若输出层激活函数为$softmax$且损失函数为交叉熵,则有$d\boldsymbol{z}^{[l]} = softmax(\boldsymbol{z}^{[l]}) - \boldsymbol{y}$,对应的求导过程如下:
- 仿照输出层的计算方式,反向传播,依次得到各层的参数更新量。
$d\boldsymbol{z}^{[l]} = softmax(\boldsymbol{z}^{[l]}) - \boldsymbol{y}$
$d{\boldsymbol{W}^{[l]}}^T = d\boldsymbol{z}^{[l]}{\boldsymbol{a}^{[l-1]}}^T$ AND $d\boldsymbol{b}^{[l]} = d\boldsymbol{z}^{[l]}$
…
$d\boldsymbol{z}^{[j]} = (\boldsymbol{W}^{[j+1]}d\boldsymbol{z}^{[j+1]}) \odot g’(\boldsymbol{z}^{[j]})$
$d{\boldsymbol{W}^{[j]}}^T = d\boldsymbol{z}^{[j]}{\boldsymbol{a}^{[j-1]}}^T$ AND $d\boldsymbol{b}^{[j]} = d\boldsymbol{z}^{[j]}$
$d\boldsymbol{z}^{[j-1]} = (\boldsymbol{W}^{[j]}d\boldsymbol{z}^{[j]}) \odot g’(\boldsymbol{z}^{[j-1]})$
…
$d{\boldsymbol{W}^{[1]}}^T = d\boldsymbol{z}^{[1]}{\boldsymbol{a}^{[0]}}^T$ AND $d\boldsymbol{b}^{[1]} = d\boldsymbol{z}^{[1]}$
$d\boldsymbol{z}^{[0]} = (\boldsymbol{W}^{[1]}d\boldsymbol{z}^{[1]}) \odot g’(\boldsymbol{z}^{[0]})$
梯度下降的数学原理
梯度下降的思路:
- 将整个模型视为一个以模型参数为自变量,以L为因变量,以样本数据为参数的函数
- 然后将模型参数寻优的问题转化为求这个函数最值和驻点的问题
- 然后基于这样一个原理自变量的数值沿梯度方向靠近时因变量的数值将随之向最值靠近,便可得到梯度下降公式:
$\boldsymbol{W} -= \alpha d\boldsymbol{W}$
$\boldsymbol{b} -= \alpha d\boldsymbol{b}$
然后根据不同的实现,又有以下的梯度下降法变种:
- 基于batch_size的不同
- batch_size = sample_size,称Batch Gradient Descent;
- batch_size = 1,称Stocastic Gradient Descent;
- batch_size介于两者之间,称Mini-Batch Gradient Descent;
- 每次不是简单的减去更新量,而是减去更新量的移动平均值,即可得到GD with Momentum;其中移动平均的含义是取前n次更新量的平均值作为本次的更新量,$n=\frac{1}{1-\beta}$,$\beta$一般取0.9;
$v^{d\boldsymbol{W}} = \beta v^{d\boldsymbol{W}} + (1-\beta)d\boldsymbol{W}$
$v^{d\boldsymbol{b}} = \beta v^{d\boldsymbol{b}} + (1-\beta)d\boldsymbol{b}$
$\boldsymbol{W} -= \alpha v^{d\boldsymbol{W}}$
$\boldsymbol{b} -= \alpha v^{d\boldsymbol{W}}$ - 在上面的基础上,如果将用更新量的平方进行移动平均,然后再对移动平均值开方得到本次的更新量,即可得到RMSprop;
$S^{d\boldsymbol{W}} = \beta S^{d\boldsymbol{W}} + (1-\beta)({d\boldsymbol{W}})^2$
$S^{d\boldsymbol{b}} = \beta S^{d\boldsymbol{b}} + (1-\beta)({d\boldsymbol{b}})^2$
$\boldsymbol{W} -= \alpha \frac{d\boldsymbol{W}}{\sqrt{S^{d\boldsymbol{W}}}}$
$\boldsymbol{b} -= \alpha \frac{d\boldsymbol{b}}{\sqrt{S^{d\boldsymbol{b}}}}$ - 将2和3合并起来使用,即可得到Adam;
$v^{d\boldsymbol{W}} = \beta_1 v^{d\boldsymbol{W}} + (1-\beta_1)d\boldsymbol{W}$
$v^{d\boldsymbol{b}} = \beta_1 v^{d\boldsymbol{b}} + (1-\beta_1)d\boldsymbol{b}$
$S^{d\boldsymbol{W}} = \beta_2 S^{d\boldsymbol{W}} + (1-\beta_2)({d\boldsymbol{W}})^2$
$S^{d\boldsymbol{b}} = \beta_2 S^{d\boldsymbol{b}} + (1-\beta_2)({d\boldsymbol{b}})^2$
$\boldsymbol{W} -= \alpha \frac{v^{d\boldsymbol{W}}}{\sqrt{S^{d\boldsymbol{W}}}+\epsilon}$
$\boldsymbol{b} -= \alpha \frac{v^{d\boldsymbol{b}}}{\sqrt{S^{d\boldsymbol{b}}}+\epsilon}$
归一化的数学原理
在向量化和Mini-Batch的前提下,每一层的中间值$Z^{[j]}$先进行跨样本的normalization之后再进行激活,就是所谓的归一化。
矩阵$Z^{[j]}$按行求算数平均,得到均值列向量$\bar{z}$;
矩阵$Z^{[j]}$与均值列向量$\bar{z}$进行标准差运算,得到标准差矩阵$\boldsymbol{\Sigma}$;
矩阵$Z^{[j]}$的每一列都减去均值列向量$\bar{z}$后,再逐元素除以标准差矩阵$\boldsymbol{\Sigma}$即可得到归一化后的新中间值矩阵。
另外归一化还存在一个小问题,就是他的前提是向量化和Mini-Batch,就是说跨样本求均值和方差的基础是有多个样本。但是在完成模型训练之后进行预测时,肯定都是每次喂到模型中一个样本,那么此时如何求均值和方差呢?毕竟最好怎么训练出来的怎么用嘛。
一般的做法是,在这个训练过程中用移动平均数实时追踪均值和方差,或者用整个训练集的均值和方差也行,问题不大,而且主流的DL框架一般都封装好了。
正则化的数学原理
正则化是一种缓解高方差,过拟合问题的措施。具体做法是在原有的损失函数之后额外增加一个关于权重矩阵的损失项,这样一来权重越大损失就越大,随着训练的进行权重会越来越趋近于0,变相地降低了模型的参数量,缓解了过拟合。
常用的两种正则化方式如下,
L1正则化
$\lvert\lvert \boldsymbol{W}^{[i]} \rvert\rvert _1$的含义是矩阵$\boldsymbol{W}^{[i]}$每个元素的绝对值的总和,被称为L1正则化,最后容易得到稀疏的权重矩阵,有利于后续的剪枝和模型压缩。对应地,由于$d\boldsymbol{W}^{[i]}$是$L$关于$\boldsymbol{W}^{[i]}$的偏导,此时有
L2正则化
$\lvert\lvert \boldsymbol{W}^{[i]} \rvert\rvert ^2_2$的含义是矩阵$\boldsymbol{W}^{[i]}$每个元素的平方的总和,被称为L2正则化,最后得到的权重矩阵较为平滑,被广泛用于防止过拟合。此时有
从L2正则权重更新的公式可以看出,相对于在不加正则的基础上,先将原矩阵乘以$1-\alpha\lambda$因子,然后在进行参数更新,因此L2正则又被称为权重衰减。
正则权重更新公式推导
本来想用矩阵求导术推导出加入正则后的$d\boldsymbol{W}^{[i]}$,但是好像不太适用。所以这里就离散的理解一下好了,比如对于L2正则,求其对于某一层的权重矩阵的偏导$d\boldsymbol{W}^{[i]}$时是不依赖于链式法则的。首先,因为求的是偏导,其它层的W项自动忽略。然后将矩阵打开来看,分别对每一个标量w求偏导,此时其他w自动忽略。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!