CNN的数学原理
二维卷积的数学原理
不管信号处理中“卷积”和“相关”的定义如何,至少在CNN中卷积的含义是明确的。就是
- 将卷积核(一个尺寸较小的方阵)与矩阵$\boldsymbol{A}$左上角对齐
- 两个矩阵逐元素相乘后求和,作为结果矩阵$\boldsymbol{B}$的左上角第一个元素
- 向右/下移动卷积核的位置,重复2,直到卷积核到达矩阵$\boldsymbol{A}$的右下角
由此带来了padding和stride的概念:
- padding:为了解决卷积带来的尺寸缩减,在卷积之前在$\boldsymbol{A}$周围补上p圈0。
- stride:卷积核每次向右/下移动s个元素。
综上,有以下公式计算卷积前后的尺寸变化:
$(n,n) and (f,f) \Longrightarrow \lfloor \frac{n+2p-f}{s}+1 \rfloor$
多维度卷积的数学原理
关键字:卷积->偏移->激活
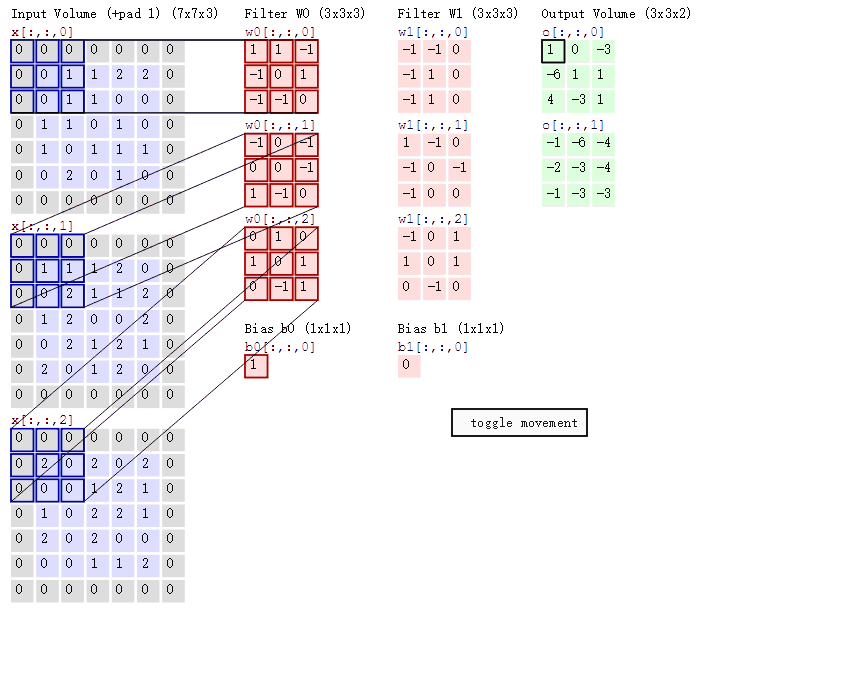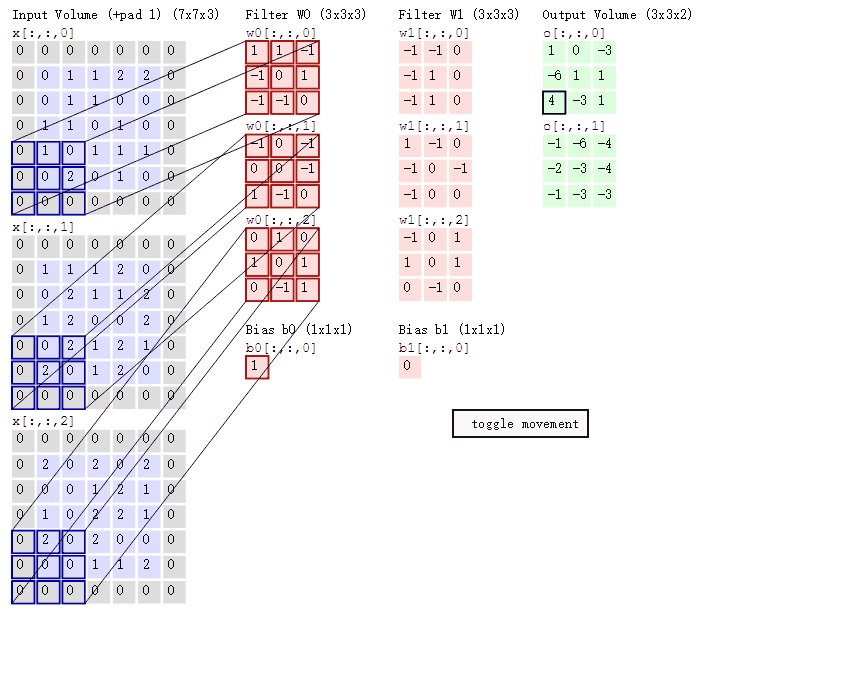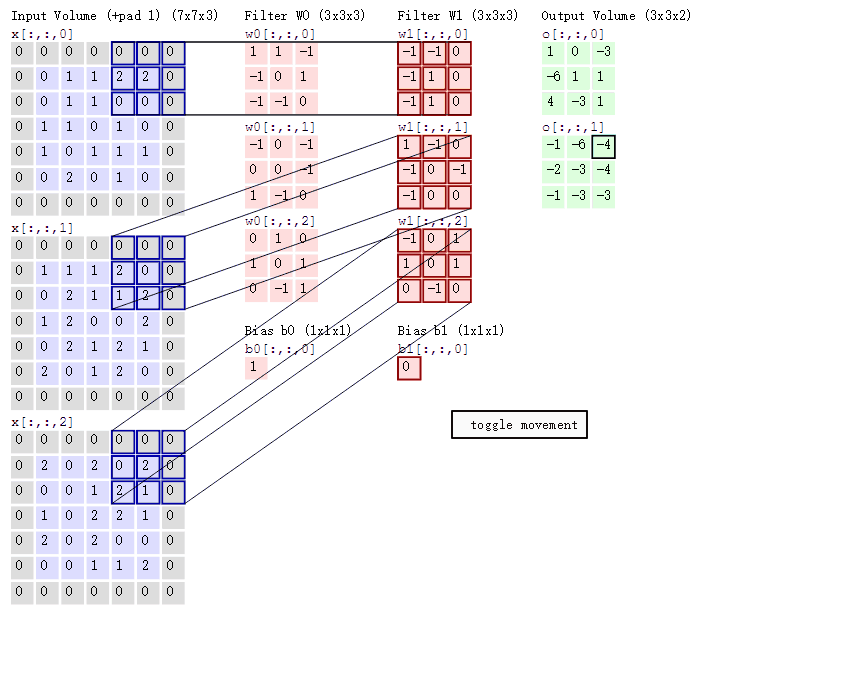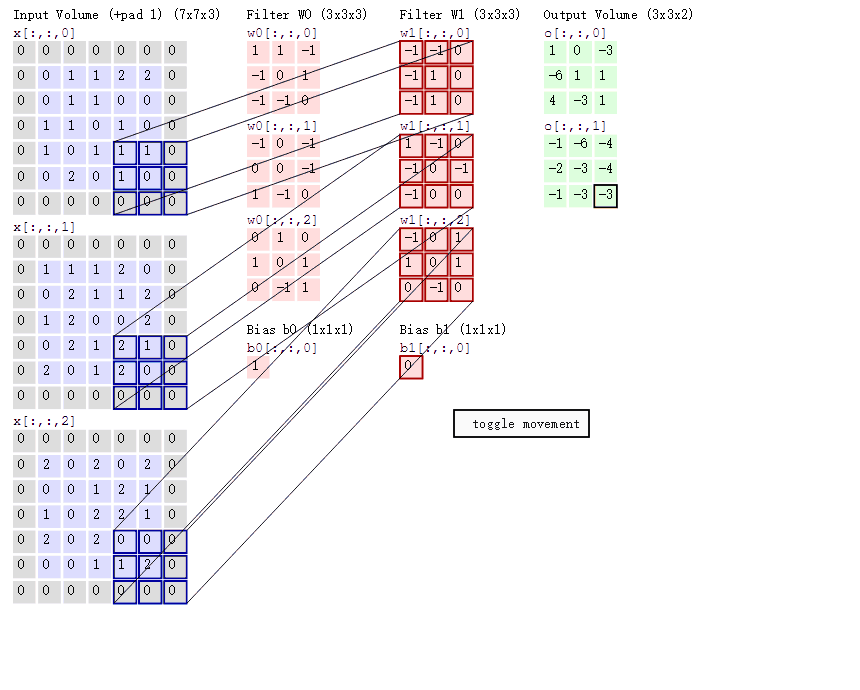
CNN模型的输入——RGB三通道图像可以看做一个三层的2D矩阵,对其卷积的含义是:
- 将一个层数相同的卷积核与这个3层的2D矩阵左上角对齐,然后做逐元素的乘积求和,并不断移动到右下角为止
- 由于求和是跨通道的,因此卷积的结果是一个单层的2D矩阵。
- 然后,仿照DNN对这个单层的2D矩阵中的每一个元素进行偏移和激活,得到作为输出的单层的2D矩阵。
- 选取另一个同尺寸的卷积核重复1-3,得到另一个单层的2D矩阵
- 将输入量与本层所有卷积核的卷积结果堆叠后,得到一个新的多层2D矩阵,作为本层的输出。
- 经过若干个卷积层处理后,将最后一个卷积层输出的多层2D矩阵看做一个列向量,将这个列向量作为$\boldsymbol{a}^{[l-1]}$,送入输出层处理。
- 若是二分类,则输出层是一个DNN神经元;若是多分类,则输出层是一个以$softmax$为激活函数的DNN网络层。此处DNN的含义指,通过矩阵乘法产生$\boldsymbol{z}^{[l]}$,而不是卷积操作。
- 显然输出的层数等于本层卷积核的数量,而输出的每一层的尺寸则由前文提及的公式计算得到。
- 与DNN不同这里的权重矩阵$\boldsymbol{W}$的维度,都是人为指定的。这也正式CNN存在的理由,减少参数。
池化的数学原理
与卷积操作的过程相同,但是每个核与输入矩阵进行的不是卷积操作,而是选取区域最大值的操作(最大池化)或者计算区域平均值的操作(平均池化)。一般用于降维。最大池化比较常用,并且一般伴随着0 padding。
CNN目标检测的基本原理
单图片,单目标
先说最简单的情形,即判断一张图片中有没有猫的问题。只需要将图片送入CNN,然后将模型输出向量定义为如下形式即可(假设待检测目标有3类)
$\hat{\boldsymbol{y}} = (p,x,y,w,h,c_1,c_2,c_3)^T$
其中
- $p$为这个result向量,或者说这个检测框存在目标的概率
- $x,y,w,h$为这个检测框的在输入图片中的位置
- $c_1, c_2, c_3$为该检测框属于各个类别的概率
单图片,多目标
如果一张图片存在多个目标——这也是实际情况中更可能发生的情况,事情就变得复杂起来。最直观并且容易理解的思路是滑动窗口搜索法:
- 定义一个尺寸的框,将输入图片的左上角与这个框对齐
- 将被框框住的部分作为“单图片,单目标”的情形处理,问题解决
- 然后移动框的位置,不断向右,向下遍历整张输入图片
- 完成遍历之后,换一个尺寸,重复1-3
- 所有尺寸都尝试过之后,输入图片中的所有目标自然被检测出来
很明显,上述做法计算量非常大,症结主要有
- 每一个框都要不断移动,遍历整张图
- 两个要穷举所有尺寸的框
对于第1个问题,可以通过滑动窗口的卷积实现来规避。而对于第二个问题,目前有两种主流思路:
- 感兴趣区域预提取的思路
- 通过图像分割,提取感兴趣区域,然后将所有感兴趣区域依次送入CNN进行预测——RCNN
- 用滑动窗口的卷积实现,代替RCNN中依次进行的CNN处理——Fast RCNN
- 用一个CNN代替图像分割进行感兴趣区域提取——Faster RCNN
- YOLO思路
将输入图片分割为19x19个区域,然后结合滑动窗口卷积实现的思路将整张图片送入CNN网络,得到19x19个$(p,x,y,w,h,c_1,c_2,c_3)^T$,每一个$(p,x,y,w,h,c_1,c_2,c_3)^T$表示对应区域中的目标检测结果。特别的,存在区域认领目标的概念,意思是说,当一个目标的检测框的中心在某个区域之内时,这个区域对应的result向量才会生成有效信息。基于这个概念,产生了以下两个问题:- 一个区域内就是有多个目标的检测框的中心点怎么办?
- 相邻的几个区域都声称同一个目标的中心点在它那里,然后都生成了几乎相同的有效的result向量怎么办?
对于问题1,采用anchor box应对,问题2则采用NMS应对。
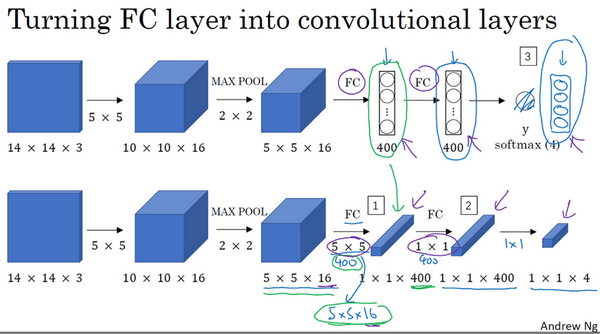
滑动窗口的卷积实现原理
将CNN网络模型中最后的几个全连接层看作卷积层。因为从数学角度看,卷积层和全连接层是一样的,因为这400个节点中每个节点的$\boldsymbol{w}$向量都可以看作一个5×5×16的过滤器,所以不论是把最后这几层看作全连接层还是卷积层,他们的输出都是上一层输出经过某个任意线性函数处理后的结果。所以本质上就是一个如何看的问题,计算的本质过程是不变的。这么做的好处是,可以把输入的19x19个区域与输出的19x19个result做有意义的关联了。
anchor box的工作原理
将某个区域认领某个目标的对应关系再细分一级,变成某个区域的某个anchor box认领某个目标。这样,当一个区域内有多个中心点时,再额外的计算一下每个目标与每个预设的anchor box之间的交并比之后,即可将目标细分到anchor box。这时,每个区域便可以认领多个不同种类的目标。一般通过聚类训练集中的目标进行anchor box的尺寸设定。
NMS的工作原理
对于所有19x19个result向量,一类一类的来看,比如先看归属于vehicle类的box:
- 选取这类box中scores最大的哪一个,记为box_best,并保留它
- 计算box_best与其余的box的IOU
- 如果其IOU>0.5了,那么就舍弃这个box(由于可能这两个box表示同一目标,所以保留分数高的哪一个)
- 从最后剩余的boxes中,再找出最大scores的哪一个,如此循环往复
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!