今天看MobileNet v2，其中为了得到“在处理低维度的特征tensor时，Relu激活函数相比于Linear激活函数在激活前后会造成更多的特征丢失”这一推论，使用了流形（manifold）的概念。所以来看看流形到底是个啥：

数学语言的定义是：流形是局部具有欧几里得空间性质的空间，在数学中用于描述几何形体。物理上，经典力学的相空间和构造广义相对论的时空模型的四维伪黎曼流形都是流形的实例。牵扯出更多新概念，比较复杂。所以这里只看machine learning中的流形概念。如下图所示，

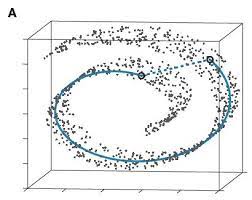
图中的每一个点，严格来讲都是一个三维的点。但是又可以明显看出这些点在三维空间中的分布是非常有规律的，基本上都集中在一个三维曲面上。基于这种现象，我们将流形理解为，高维空间中一个可变换成低维空间的子空间，例如上图，这个曲面作为一个三维曲面其实可以变换为一个二维平面。

对于机器学习和深度学习领域的数据，一般数据因为固有的特性（比如在不同光照条件下的同一张人脸的灰度图像），导致无法“填满”整个高维空间。例如如果数据只能出现在三维空间中的一个球面上。那这个球面以外的空间永远不会有数据点。而一个表面我们完全可以只用两个参数来表示(经度、维度)。

这样在聚类求样本间的相似距离时，就有了两种方式。一种是在流形的高维空间中求，即图中直线。另一种是在流形展开后的低维空间中求，即图中的曲线。具体用途，后面谈到再说吧。mark

参考链接：
[1] https://www.zhihu.com/question/24015486/answer/194284643