写在前面

一种较为特殊的概率累加理论框架，适用场景可以抽象为：

存在一个事件Q，事件Q的真实情形有一系列可能的状态{A,B,C}。对于Q取A，还是B，还是C，多个独立的观测系统给出了不同的概率分布情况。如何平衡多个观测系统的概率分布，便是DS理论所要解决的问题。

可以看出，该理论天然适用于多传感器信息融合。Apollo中即采用了该理论用于合成Lidar/Camera/Radar检出障碍物的Existence Probability和Type Probability。

基本概念

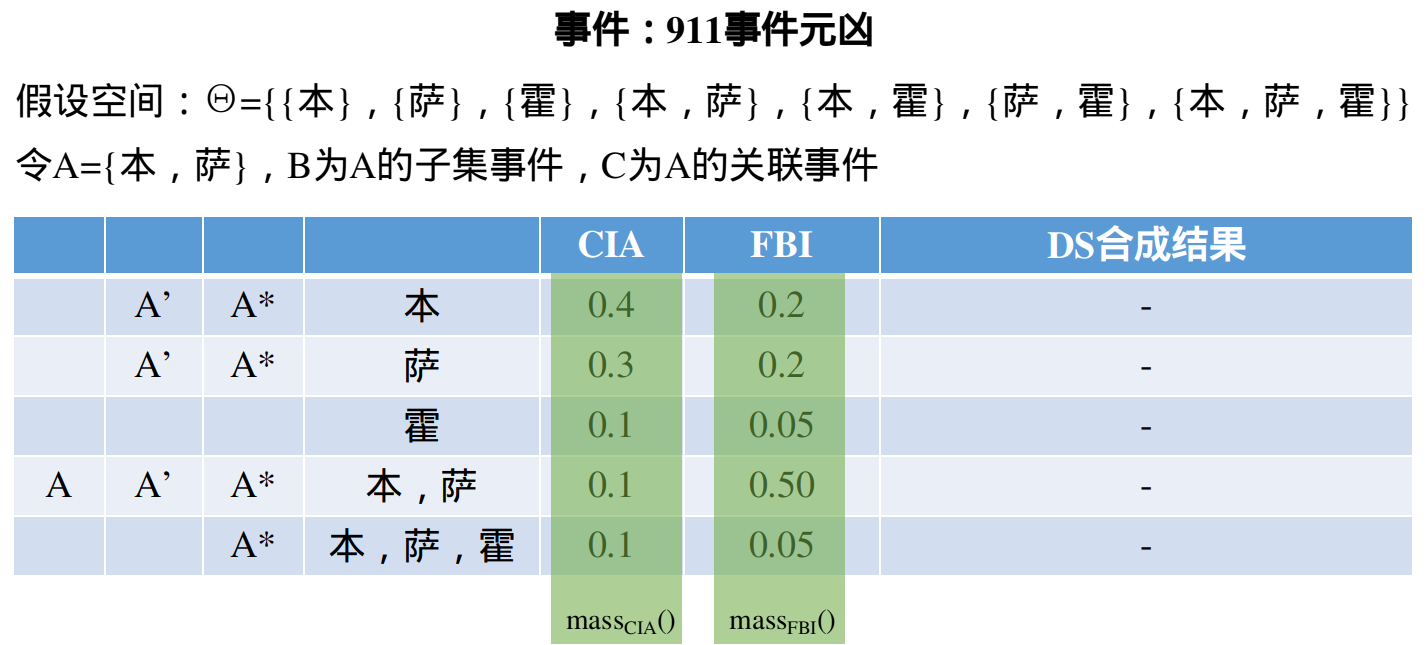
首先明确以下基本概念的数学意义：

• 假设空间：事件的”可能事件”的集合
• mass函数：定义域为假设空间，值域为[0, 1]的离散函数。其实就是一个观测系统对于该事件假设空间所给出的概率分布。
• 信任函数：对于假设空间中的一个元素A，其信任函数值定义为所有A的子集元素基于某一个观测系统的mass函数值之和。代入上例，
  基于CIA观测系统： $$bel_{CIA}(A) = mass_{CIA}({本}) + mass_{CIA}({萨}) + mass_{CIA}({本,萨})$$ $$= 0.4+0.3+0.1 = 0.8$$ 基于FBI观测系统： $$bel_{FBI}(A) = mass_{FBI}({本}) + mass_{FBI}({萨}) + mass_{FBI}({本,萨})$$ $$= 0.2+0.2+0.5 = 0.9$$
• 似然函数：对于假设空间中的一个元素A，其似然函数值定义为所有A的关联元素基于某一个观测系统的mass函数值之和。其中关联事件指与A交集不为空的事件。代入上例
  基于CIA观测系统： $$Pl_{CIA}(A) = mass_{CIA}({本}) + mass_{CIA}({萨}) + mass_{CIA}({本,萨}) + mass_{CIA}({本,萨,霍})$$ $$= 0.4+0.3+0.1+0.1 = 0.9$$ 基于FBI观测系统： $$Pl_{FBI}(A) = mass_{FBI}({本}) + mass_{FBI}({萨}) + mass_{FBI}({本,萨}) + mass_{CIA}({本,萨,霍})$$ $$= 0.2+0.2+0.5+0.05 = 0.95$$
• 信任区间：对于假设空间中的一个元素A，其信任区间定义为$[Bel(A), Pl(A)]$。

Dempster合成规则

现在来看，如何合成两个或多个mass函数。Dempster给出的公式为：

$$K=\sum_{A_1 \cap A_2 \cap...\cap A_n \neq \emptyset} m_1(A_1) \cdot m_2(A_2)...m_n(A_n)$$ $$(m_1 \oplus m_1)(A) = \frac{1}{K} \sum_{A_1 \cap A_2 \cap...\cap A_n = A} m_1(A_1) \cdot m_2(A_2)...m_n(A_n)$$

从第一个公式可以看出，$K$的值与$A$无关，与各个观测系统针对假设空间给出的整体概率分布有关。有$n$个观测系统（或者说mass函数）就从状态空间中找到$n$个事件作为一个集合，这个集合需要满足，其所有元素的总交集为空集。找到所有这样的集合，将这些集合的全排列依次代入各个mass函数，求总和，即为K。

第二个公式的理解方式跟第一个类似，不过这次选取集合的标准是所有$n$个元素的交集为$A$。

总结

DS证据合成理论的核心在于Dempster合成规则，而Dempster合成规则的关键在于事件之间的交集运算。这一点在Apollo的源码中得到了非常具有普适性的实现。