相机成像原理

针孔模型的成像原理

相机的成像原理可以借助下图所示的针孔模型来加以解释：

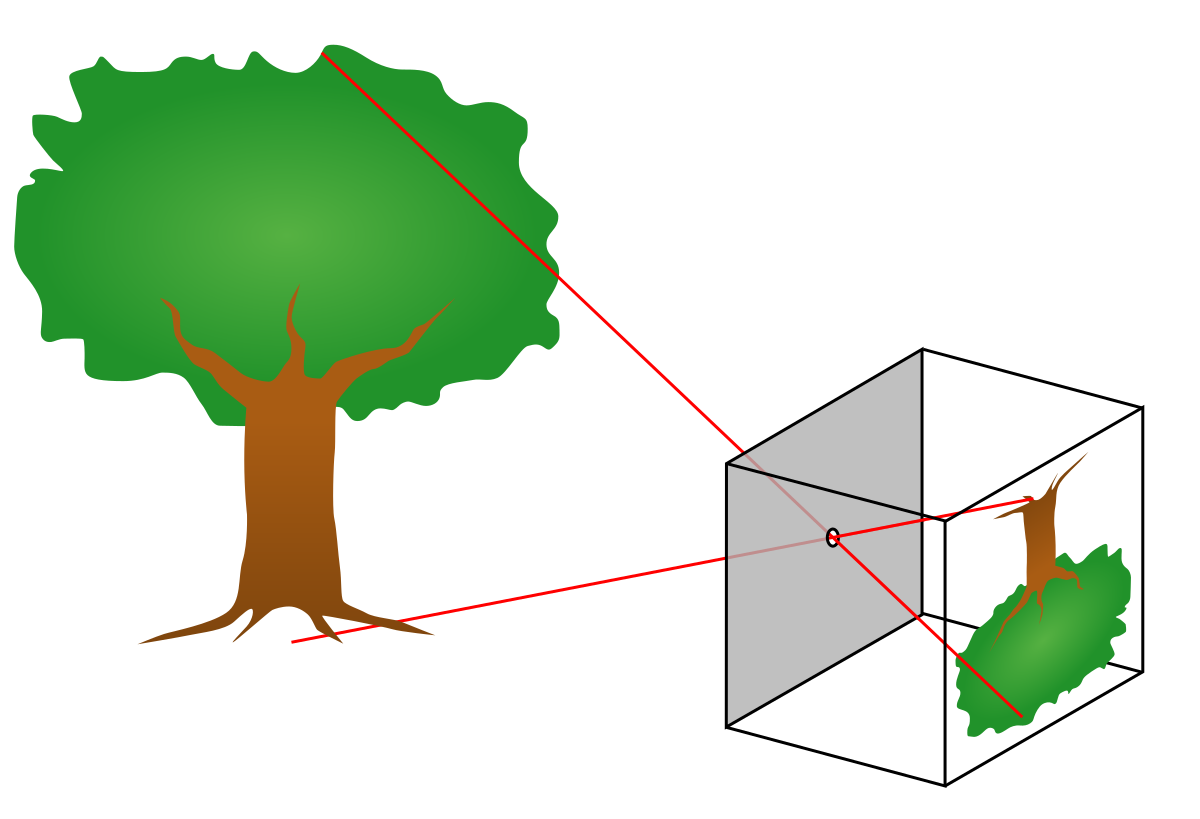
假设在一个空间中，只包含光源、树和感光白板三个物体。当光源发出的光打在的树上时，会发生漫反射现象。即，反射光线会以树上任一点为球心射向所有方向。

此时如果只是简单地在树的前方放置一个感光白板，以白板上的任意一个点A为研究对象，该点将收到来自树上所有反射点的反射光线。这些光线叠加在一起，将使得感光点A无法专一地只体现某一个反射点的特征。宏观来看，感光白板上无法产生任何关于这棵树的有效视觉信息。

如果在树和感光白板之间加一个针孔板，那么感光点A的光线来源就只有树上的一个反射点了，并且反射点-针孔-感光点三点成一线。这样，宏观来看，感光白板上便产生了一棵树。

相机坐标系

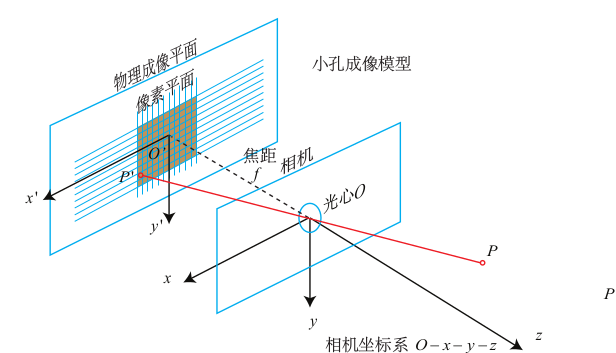
盘点上述成像过程中涉及的坐标系，一般有以下4个：

  1. 世界坐标系，以相机所在的物理世界中的某个点为坐标原点（比如车辆的后轴中心），其中一点记作$(X_w,Y_w,Z_w)^T$；
  2. 相机坐标系，以光心(针孔)为坐标原点，其中一点记作$(X_c,Y_c,Z_c)^T$；
  3. 图像物理坐标系，以光心在感光板上的对应位置为坐标原点，其中一点记作$(x,y)^T$；
  4. 图像像素坐标系，一般以图像的左上角为坐标原点，其中一点记作$(u,v)^T$，并且单位不再是长度，而是像素个数；

坐标系转换关系

鉴于“反射点-针孔-感光点三点一线”的几何特征，给定一个世界坐标系中的点$(X_w,Y_w,Z_w)^T$，是可以求得该点在图像像素坐标系中的坐标的。

1.世界坐标系-相机坐标系

两个坐标系之间是简单地旋转和平移关系，因此有：

可以看到，式中的转换参数与相机本身的属性并无关系，因此一般将该矩阵称作相机的外参。

2.相机坐标系-图像物理坐标系

从相机坐标系到图像物理坐标系的转换关键点在于，这是一个3D-2D的转换，并且存在一个由相似三角形产生的缩放关系。因此有：

其中f为相机焦距，可以看到，这个转换是不可逆的，因此我们称单目相机损失了深度信息。

3.图像物理坐标系-图像像素坐标系

这是一个2D-2D的转换，而且在同一个平面上，只是坐标原点和坐标的单位需要转换。因此有：

其中，在x方向上，每个像素的尺寸为$d_x$毫米；$u_0$指光心在从左数第$u_0$个像素上。

4.汇总

综合来看，先将2和3结合，得到：

其中$\boldsymbol{K}$中的参数只跟相机属性相关，称作相机的内参，是一个3x3的矩阵。

然后，再加上1中的外参，得到：

其中$\boldsymbol{E}$为相机外参，是一个3x4矩阵。