逆透视映射(InversePerspectiveMapping)
前言
众所周知,真实世界的三维坐标在向相机的成像平面上投影时,会损失深度信息,使得整个过程不可逆。也就是说,已知图像中一个点的坐标$(u,v)$是无法求得该点在真实世界的三维坐标$(X_w, Y_w, Z_w)$的。
那么,如果额外多给一项信息,即现在关心的所有三维世界的点都是同在一个平面(比如路面上的车道线)上呢?此时图像像素坐标系和世界坐标系之间的坐标转换就变成了可逆关系。
这种情形下,从像素坐标系坐标得到世界坐标系坐标的做法称作逆透视映射。
应用一:同一物理平面在两幅图像之间的转换
现有:
- 一个物理世界的平面,称作$P$
- 两个不同位置的相机,称作$A$和$B$
- $P$在$A$的成像平面上的投影,称作$P_A$,其上一点在$A$的像素坐标系上的坐标记作$(u_A,v_A)$
- $P$在$B$的成像平面上的投影,称作$P_B$,其上一点在$B$的像素坐标系上的坐标记作$(u_B,v_B)$

那么,$P_A$和$P_B$之间互为投影变换(单应性变换),这意味着存在一个3x3的可逆矩阵$\boldsymbol{H}$,使得:
矩阵$\boldsymbol{H}$中的9个元素的取值可以通过在两幅图像中取4组不共线的对应点解方程得到,也可以通过两个相机内外参矩阵之间的关系得到。
应用二:车道线物理坐标的求解
道路平面上的车道线上的点在世界坐标系中的坐标,与对应点在前视相机像素坐标系中的坐标之间,同样存在上述单应性变换关系。这一点可以从下面的公式推导过程中得到:
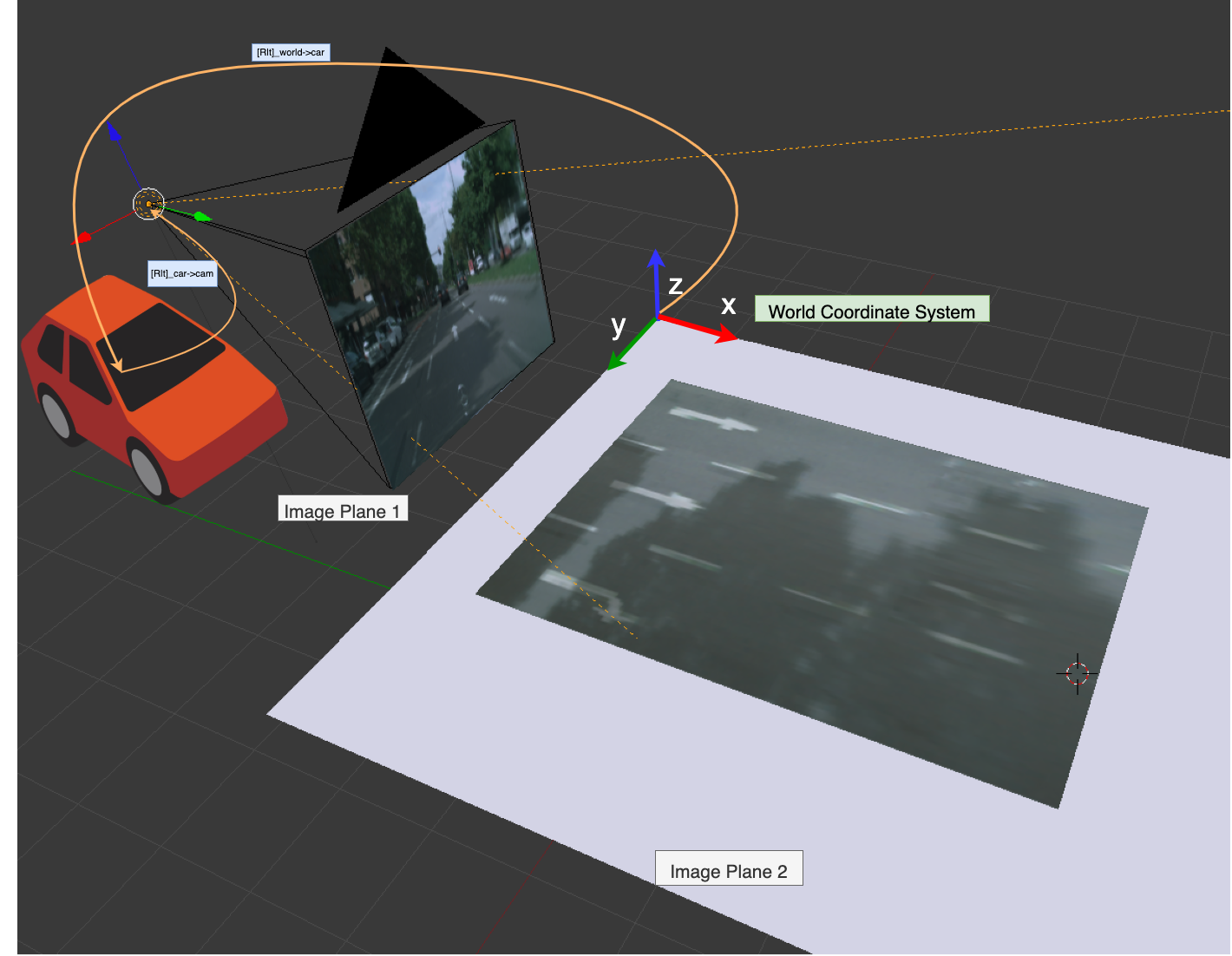
首先,图像像素坐标系和世界坐标系之间的坐标转换关系如下:
在这个应用场景下有,$Z_w=0$,因此有:
合并内外参矩阵得:
注意到,$\boldsymbol{H}$矩阵中的第三列元素其实是无效的,因此有:
上式中,可以看到$\boldsymbol{H}$矩阵的前两列由内参矩阵和旋转矩阵相乘得到,第三列由内参矩阵和平移向量相乘得到。这也是apollo代码中,用conceptual方式求取透视投影矩阵所基于的原理。
这样,用$\boldsymbol{H}$的逆矩阵与像素坐标点相乘,然后归一化Z坐标,即可得到像素坐标点在世界坐标系中的XY坐标。
参考
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!