二维直角坐标系

记录一个经常遇到的问题：

已知:

• 一个点A在直角坐标系XOY下的坐标为$(x,y)$;
• 另一个直角坐标系X’O’Y’的原点O’在XOY下的坐标为$(x_0, y_0)$，旋转角为$\theta$（逆时针旋转为正）;

求解：

• 点A在X’O’Y’下的坐标$(x’, y’)$

推导：

主要通过三角函数的合角公式来求解。

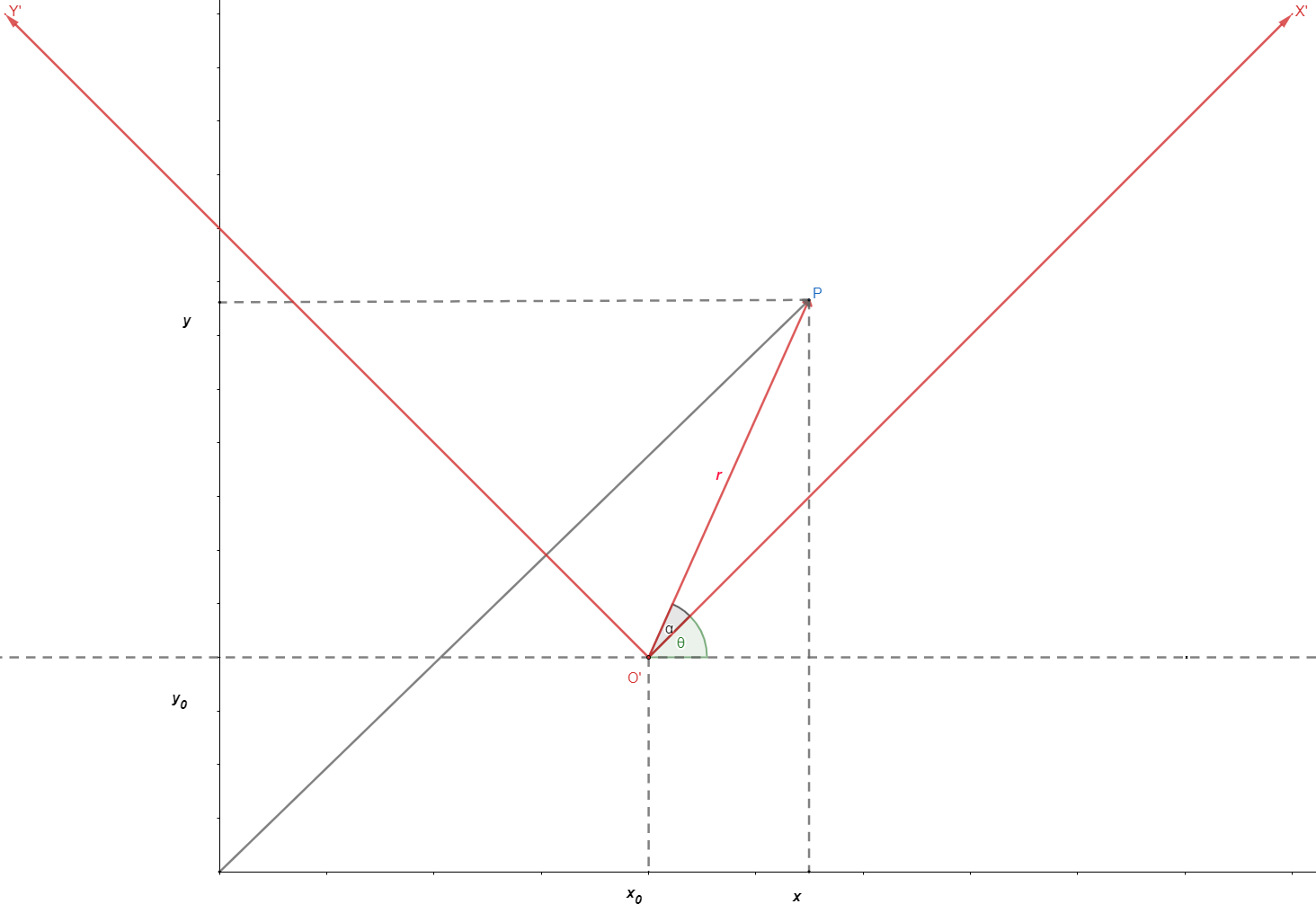
根据上图，有:

$$x - x_0 = rcos(\alpha + \theta) = rcos \alpha cos \theta-rsin \alpha sin \theta = x'cos \theta - y'sin \theta$$ $$y - y_0 = rsin(\alpha + \theta) = rsin \alpha cos \theta+rcos \alpha sin \theta = y'cos \theta + x'sin \theta$$

通过等式两边同时乘$sin \theta$或$cos \theta$，然后两式相加又可以得到:

$$x' = (x - x_0)cos \theta + (y - y_0)sin \theta$$ $$y' = -(x - x_0)sin \theta + (y - y_0)cos \theta$$

总结:

上面的两组公式用于，将一个点在A坐标系下的坐标转换到另一个坐标系，这个计算显然是可逆且对称的。所以要选取哪一种公式进行计算的关键在于识别清楚，谁是XOY，谁又是X’O’Y’。

即，

已知P in A和A in B，求P in B时，用第一组公式;

已知P in A和B in A，求P in B时，用第二组公式。